When making music it can help to know how music theory works. That’s why we’ve put together this Essential Music Theory cheat sheet-style guide for artists which details everything from note names and accidentals to scale degrees and solfege syllables, important scales, chords and progressions, and much more.
This free unit covers the most essential music theory knowledge necessary for producers, songwriters, instrumentalists, singers, and others. If you’d like to learn how to create world-class music first hand from our industry professional instructors, then be sure to enroll in one of our pointblank Los Angeles courses.
Want to learn more about our programs in LA? Then be sure to attend our next pointblank Los Angeles Open House by signing up here.
TABLE OF CONTENTS
- ELEMENTS OF MUSIC
- NOTE NAMES & ACCIDENTALS
- THE TWELVE NOTES IN THE OCTAVE
- SCALE DEGREES & SOLFEGE SYLLABLES
- HALF STEPS AND WHOLE STEPS
- THE MAJOR SCALE FORMULA
- OTHER IMPORTANT SCALES
- ALL ABOUT INTERVALS
ELEMENTS OF MUSIC
The most important elements within music are: pitch, rhythm, dynamics, timbre, and form.
- Pitches are sonic frequencies, also known in music as notes. Pitches can be organized “horizontally” through melody (i.e. linearly, as in the “topline”) and “vertically” through harmony (as in a “block chord”).
- Rhythm includes all aspects of time and timing in music. Important rhythmic considerations include pulse, tempo, meter, note duration, articulation, and syncopation.
- Dynamics refer to the volume, expression, and phrasing of a musical gesture.
- Timbre is the unique tone quality or color of a sound, shaped by its higher harmonics or overtones. The timbre of an instrument or sound source distinguishes it from other sounds.
- Form, also known as structure, refers to the different sections of a musical composition and their function, order, and transitions between them.
NOTE NAMES & ACCIDENTALS
A sound source actually moves air molecules in compressions and rarefactions and creates a a specific frequency, an exact rate of vibration , which is perceived by our ears as a distinct pitch and known in music as a note. Pitches can be described scientifically in cycles per second (cps), more commonly known as Hertz (Hz). The standard pitch most modern musicians tune to is 440 Hz, known as A=440, which means that when sound waves hit our ear drum at 440 times each second, our brain perceives a pitch which musicians identify as the musical note A.
However, the first note most musicians learn to find on the piano is called middle C (also known as C4, or sometimes C3 in the realm of MIDI). To find middle C, start by noticing how black keys come in repeated sets of two and three. We can look for the set of two black keys in the middle of the keyboard and find the white key directly to the left of the two black keys. This is middle C.

The first seven letters of the alphabet ( A, B, C, D, E, F, and G ) are used to name musical notes. The sharp ( ♯ ) and flat ( ♭ ) symbols are also used in certain note names; they are known as accidentals. The sharp raises a note, and flat lowers it. The black keys on the piano are named C#, D#, F#, G# and A# – there are no black keys reserved for B# or E#. Alternatively, we can name the black keys with flats: D♭, E♭, G♭, A♭, and B♭, and see how there are no black keys reserved for C♭ or F♭. This is easiest to grasp by looking at the piano, and observing how there is no black key found between the notes B and C, or between E and F.
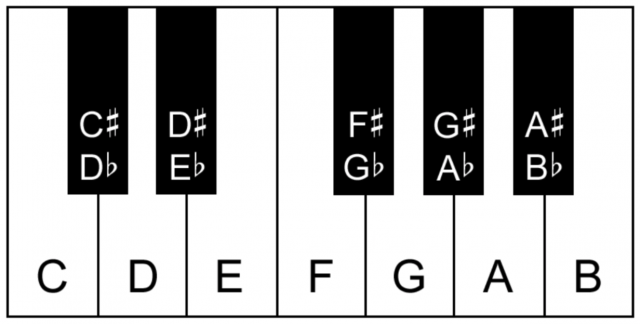
THE TWELVE NOTES IN THE OCTAVE
As seen above, there are twelve possible unique musical notes (a.k.a. pitch classes) and they repeat in octaves – a full-size piano has 88 keys and consists of about 7 1⁄2 octaves. Each of the twelve possible notes has multiple appropriate names depending on its context. Out of these twelve possible notes, only seven of them are found in the major scale. If we think of one octave as a set of twelve boxes (rather than the keyboard’s layout), we can clearly see which seven boxes are selected to form the major scale:
TWELVE NOTES IN THE OCTAVE – SEVEN IN THE MAJOR SCALE
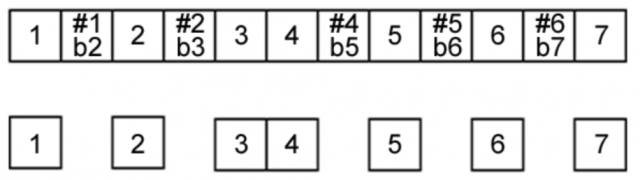
As you can see, we don’t number the twelve possible notes as 1 through 12. Only the seven notes that comprise the major scale are given scale degrees of 1 through 7. The five notes not found in the major scale are given sharp or flat scale degrees which reference their neighbors in the major scale. In this way, we can see how the major scale is the default mental map for music theory, and we should learn it well!
SCALE DEGREES & SOLFEGE SYLLABLES
There are three main labels we can apply to musical notes:
- Letter names (C, D, E, F, G, A, B, and others such as C#, Eb, F#, Ab, and Bb)
- Scale degrees (1, 2, 3, 4, 5, 6, 7, and others such as♭2,♭3, #4,♭6 and♭7)
- Solfege syllables (do, re, mi, fa, sol, la, ti, and others such as di, ra, ri, me, fi, se, si, le, li, te, and ta).
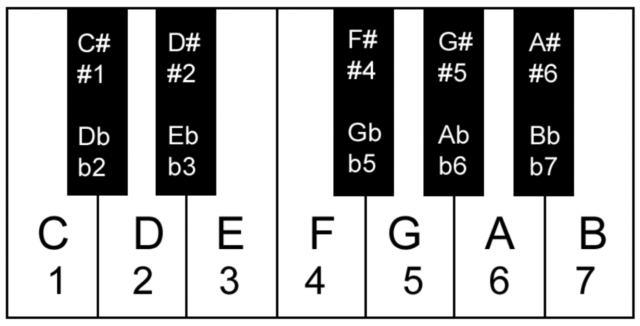
Letter names never change their position on the keyboard. However, scale degrees and solfege syllables are movable. Scale degree 1 will not always be C; it may be F, Bb, or any other one of the twelve possible pitches that we decide to start our major scale on!
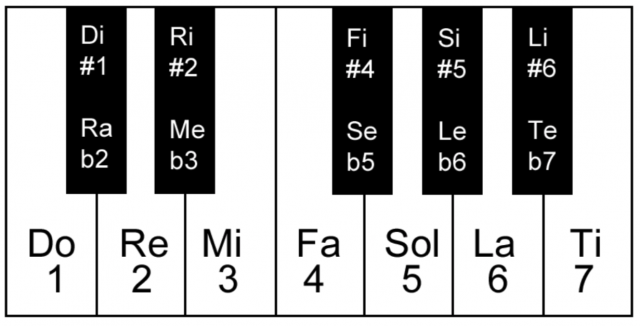
Solfege syllables are essentially easily-singable equivalents to scale degrees, and they are also movable. Do will not always be C; it may be Eb, F#, or any other of the twelve possible pitches. However, Do is always scale degree 1, and vice versa.
One octave of piano keys, labeled with note names and scale degrees:
One octave of piano keys, labeled with solfege syllables next to their equivalent scale degrees:
HALF STEPS AND WHOLE STEPS
The half step (a.k.a. semitone) is our name for the distance between one note and the very next note, the smallest building block of music. On the piano, there are black-to-white-key half steps and white-to-black-key half steps, and even a couple white-to-white-key half steps, but there are no black-to-black-key half steps.
A whole step (a.k.a. tone or whole tone) is equivalent to two half steps. Whole step is the name given to the distance between two notes that have one and only one note in between them.
THE MAJOR SCALE FORMULA
A scale is a sequence of musical notes conceptualized in ascending and/or descending order. Let’s start with the major scale, which has birthed the majority of popular music, and is the default scale for all music theory studies. Learning to build the major scale is the first real benchmark in one’s understanding of music theory. To create a major scale, we pick any starting note, known as the tonic, and we follow it with this magic formula of whole steps and half steps:
Whole Whole Half Whole Whole Whole Half
This can be abbreviated: W W H W W W H.
As you can see, the major scale consists mostly of whole steps, with half steps appearing only between the 3rd and 4th notes of the scale and the 7th and 8th notes of the scale. Also, the 8th note in the scale is an octave repetition of the 1st note in the scale (scale degree 8 = 1) . This means that there are only 7 unique pitches in the major scale, even though we frequently perform it as an 8-note scale which starts and ends on the tonic note. All scales repeat in higher or lower octaves, ascending or descending as far as you like.
Now that we know how to build the major scale, we can create a table which spells out the note names found in every possible major scale. The main rule to remember when spelling notes within a major scale is that we cannot use the same letter name twice within one major scale. For example, F and F# cannot belong to the same scale; we must either rename F as E# or rename F# as G♭. It is also important to remember that a major scale can contain either sharps or flats, but not both at the same time.
TABLE OF MAJOR SCALES
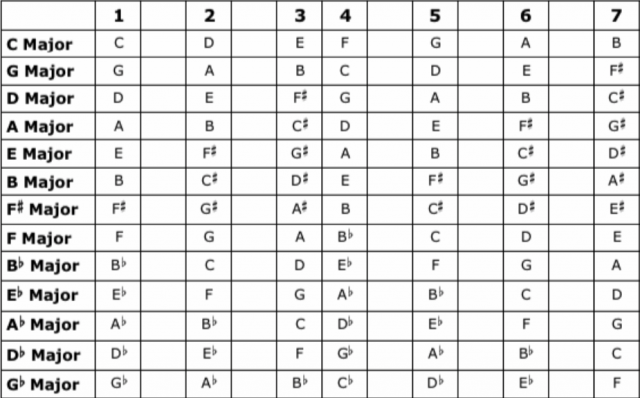
As you can see above, each major scale has a unique number of sharp or flat notes used:
C = 0
G = 1 #
D = 2 #
A = 3 #
E = 4 #
B = 5 #
F# = 6 #
F = 1♭
B♭ = 2♭
E♭ = 3♭
A♭ = 4♭
D♭ = 5♭
G♭ = 6♭
This means that we can describe a major scale, also known as a major key, by indicating the number of sharps or flats it has. This is known as its key signature.
OTHER IMPORTANT SCALES
- The scale built using only half steps (the collection of all twelve notes in the octave) is known as the chromatic scale.
- Using only whole steps, we get the whole tone scale (C, D, E, F♯, G♯, and A♯).
The chromatic scale and the whole tone scale are considered synthetic scales, and since they don’t have a mixed map of whole steps and half steps to help us orient ourselves, they are very disorienting! They have a very lost, uprooted, drifting, ambiguous sound to them, and for this reason they are often used to score dream sequences within TV shows and movies.
Here is a comprehensive list of many more very colorful scales you may wish to explore:
PENTATONIC SCALES:
- Major Pentatonic = 1 2 3 5 6
- Minor Pentatonic = 1 ♭3 4 5 ♭7
MINOR SCALES:
- Natural Minor = 1 2 ♭3 4 5 ♭6 ♭7
- Harmonic Minor = 1 2 ♭3 4 5 ♭6 7
- Melodic Minor = 1 2 ♭3 4 5 6 7
THE SEVEN DIATONIC MODES:
- Ionian = 1 2 3 4 5 6 7 (a.k.a. Major Scale)
- Dorian = 1 2 ♭3 4 5 6 ♭7 (a.k.a. Minor ↑6)
- Phrygian = 1 ♭2 ♭3 4 5 ♭6 ♭7 (a.k.a. Minor ↓2)
- Lydian = 1 2 3 #4 5 6 7 (a.k.a. Major ↑4)
- Mixolydian = 1 2 3 4 5 6 ♭7 (a.k.a. Major ↓7)
- Aeolian = 1 2 ♭3 4 5 ♭6 ♭7 (a.k.a. Minor Scale)
- Locrian = 1 ♭2 ♭3 4 ♭5 ♭6 ♭7 (a.k.a. Minor ↓2↓5)
JAZZ, BLUES, & EXOTIC SCALES:
- Blues Scale = 1 ♭3 4 #4 5 ♭7
- Bebop Major Scale = 1 2 3 4 5 #5 6 7
- Bebop Dominant Scale = 1 2 3 4 5 6♭7 7
- Diminished Scale = 1 2 ♭3 4 ♭5 ♭6 6 ♭7
- Acoustic Scale = 1 2 3 #4 5 6 ♭7 (a.k.a. Lydian Dominant)
- Double Harmonic Major = 1 ♭2 3 4 5 ♭6 7 (a.k.a. Phrygian Major)
- Superlocrian = 1 ♭2 ♭3 ♭4 ♭5 ♭6 ♭7 (a.k.a. Altered Scale)
ALL ABOUT INTERVALS
An interval is a specific distance between two notes. The half step and the whole step, which we referred to as the smallest building blocks in music, are examples of small intervals, except that properly-named intervals consist of two words: a type and an amount, also thought of as a quality and a quantity. A half step is properly named a minor second and a whole step is a major second. In this context, minor or major is the interval type or quality, and second is the amount, or quantity. Intervals larger than a major second can be built by adding more half steps. Interval names are determined by counting the number of half steps between two notes. An interval can be performed melodically (two notes sounding one after the other) or harmonically (two notes sounding at the same time).
INTERVALS IN THE MAJOR SCALE
A good first step towards grasping intervals is to examine which intervals occur naturally in the major scale. If we think in the key of C major and consider the distance from the tonic note going upwards to each other note in the major scale, the intervals are:
- C up to D = Do up to Re = major second (M2)
- C up to E = Do up to Mi = major third (M3)
- C up to F = Do up to Fa = perfect fourth (P4)
- C up to G = Do up to So = perfect fifth (P5)
- C up to A = Do up to La = major sixth (M6)
- C up to B = Do up to Ti = major seventh (M7)
- C up to C = Do up to Do = perfect eighth (P8)
Other intervals are found if we measure them from the tonic downwards to the other notes in the key:
- C down to B = Do down to Ti = minor second (m2)
- C down to A = Do down to La = minor third (m3)
- C down to G = Do down to So = perfect fourth (P4)
- C down to F = Do down to Fa = perfect fifth (P5)
- C down to E = Do down to Mi = minor sixth (m6)
- C down to D = Do down to Re = minor seventh (M7)
- C down to C = Do down to Do = perfect eighth (P8)
The five possible interval types are perfect, major, minor, diminished, and augmented; these types can be abbreviated as P, M, m, d, and A respectively. They are divided into two camps:
PERFECT INTERVALS (U, 4, 5, 8)
d < P < A
MAJOR/MINOR INTERVALS (2, 3, 6, 7)
d < m < M < A
When you begin to tamper with an interval by shrinking or enlarging it by a half step at a time, the interval type changes. A perfect interval if enlarged by one half step becomes an augmented interval, and if shrunk by one half step becomes a diminished interval, but a perfect interval can never become a major or minor interval, and vice versa. A major interval if enlarged by one half step becomes augmented, and if shrunk by one half step becomes a minor interval, and if shrunk by two half steps becomes a diminished interval. So perfect intervals, when tampered with, move straight to either the diminished or augmented type, whereas major and minor intervals may have an extra type to pass through before reaching the diminished or augmented type, depending on which interval you start with.
MASTER INTERVAL CHART
Remember: All intervals must be named with both their quality and their quantity!
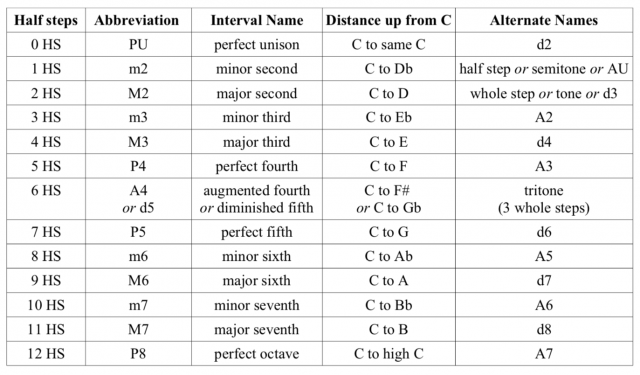
METHOD FOR NAMING INTERVALS
1. Count letter names to determine the quantity first. Count all letter names including the first note. Quantity is the interval’s general size: unison, second, third, fourth, fifth, sixth, seventh, and octave (a.k.a. eighth) are the possible quantities within one octave.
2. Count half steps and check the Master Interval Chart shown above to determine the quality. Don’t count the first note alone – it’s not a half step until you reach the second note!
Intervals can be any size, including amounts much larger than the ones we have discussed thus far, but after one octave (eighth) we can hear that a ninth resembles a second in its sound, a tenth resembles a third, etc. We can say that an eleventh shares the same quality as a fourth, but has been displaced by one octave, or that a twelfth is like a fifth with an octave displacement.
9th = 2nd
10th = 3rd
11th = 4th
12th = 5th
13th = 6th
14th = 7th
Each interval has a unique sound, a particular flavor we can learn to identify through ear training practice, and which we can sing with solfege syllables. Excellent ear training utilities are available online for free, such as musictheory.net’s Interval Ear Trainer. Even so, mastering intervals can take a long time, and the richness found in intervallic relationships is deep and can be enjoyed for a lifetime. The stable, pleasing intervals are known as consonances, and the unstable, tense intervals are known as dissonances. There is mystery and magic in the various degrees of intervallic consonance and dissonance, and this is the wellspring of harmony that yields the vast majority of popular music!
Now that you’ve got music theory down to a T, why not put it into action by writing your own song? If you need any help composing in electronic DAWs using state-of-the-art studios, software, and expertise, don’t hesitate to check out our courses in London, LA and Online.
Daniel Brummel holds the Bachelor of Arts degree in Music Composition from the University of California, Los Angeles (UCLA) and the Master of Music degree in Commercial Music Composition from California State University, Los Angeles (CSULA). He serves as the Chief Academic Officer at pointblank Los Angeles.
Register to Access Free Courses, Plugins, Projects, Samples & More
When you register with pointblank, you access an array of free sounds, plugins, online course samples and much more! Simply register below and visit our Free Stuff page to get your hands on a range of exclusive music-making tools and tutorials provided by the team. Fill your boots!
